Oneindig diepe put (infinite square well)

De oneindig diepe potentiaalput is een quantummechanisch systeem dat we exact kunnen oplossen. Het systeem bestaat uit een deeltje dat zich bevindt in een ééndimensionale potentiaalput met wanden die oneindig hoog en oneindig steil zijn. Voor een put die loopt van \(x=0\) tot \(x=a\) kunnen we deze potentiaal uitdrukken als:

\[ V(x) = \begin{cases} \ 0 & \text{voor } 0 \leq x \leq a,\\ \ \infty & \text{elders.} \end{cases} \]

De eigentoestanden van de oneindig diepe potentiaalput zijn:

\[ \psi_n(x) = \sqrt{\frac{2}{a}}{\rm sin}\left(\frac{n\pi x}{a}\right), \]

met bijbehorende eigenenergieën:

\[ E_n = \frac{n^2 \pi^2 \hbar^2}{2ma^2}, \]

waarbij \(n=1,2,...\). Het getal \(n\) geeft dus feitelijk het aantal buiken aan dat de golffunctie heeft. Hieronder zie je de eerste drie eigentoestanden \(\psi_n(x)\) en de waarschijnlijkheidsverdelingen \(|\psi_n(x))|^2\) die daarbij horen.

import numpy as np
import matplotlib.pyplot as plt

n = 256
x = np.linspace(0,1,n)
y1 = np.sin(1*np.pi*x)
y2 = np.sin(2*np.pi*x)
y3 = np.sin(3*np.pi*x)

fig = plt.figure(figsize=(5, 2.5))
plt.xlabel ('$x/a$')
plt.ylabel ('$\psi_n(x)$')
plt.plot (x, y1)
plt.plot (x, y2)
plt.plot (x, y3)
plt.legend(('$\psi_1$','$\psi_2$','$\psi_3$'))
plt.show()

fig = plt.figure(figsize=(5, 2.5))
plt.xlabel ('$x/a$')
plt.ylabel ('$|\psi_n(x)|^2$')
plt.plot (x, y1*y1)
plt.plot (x, y2*y2)
plt.plot (x, y3*y3)
plt.show()

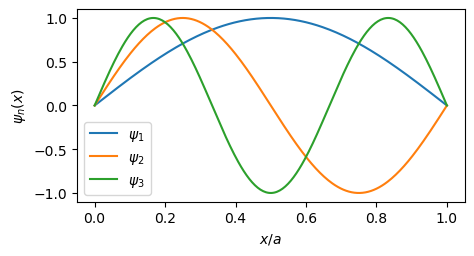
De toestanden \(\psi_n(x)\) vormen een volledige set. Dat wil zeggen dat je met lineaire combinaties van deze toestanden elke mogelijke toestand \(\psi(x)\) binnen de put kunt maken (waarbij altijd de randvoorwaarde \(\psi(0) = \psi(a) = 0\) geldt). Elke toestand (mits genormaliseerd) is in principe een geldige quantumtoestand. Maar alleen de toestanden \(\psi_n(x)\) zijn eigentoestanden van de Hamiltoniaan. Dus alleen voor die toestanden is de energie bepaald en alleen die toestanden zijn stationair in de tijd.

Op het moment dat we de oneindig diepe potentiaalput beschouwen als onverstoord systeem waarop een verstoring wordt toegepast, dan duiden we bovenstaande toestanden en energieën aan met \(\psi_n^0(x)\) en \(E_n^0\).