Clebsch Gordan coëfficiënten¶

Nadat je het impulsmoment hebt bestudeerd is het interessant om te kijken wat er gebeurt als je twee impulsmomenten optelt. Je zal dit namelijk regelmatig tegenkomen. Bij dit systeem heb je namelijk verschillende bases waaruit je moet kiezen. Dat maakt het interessant om het te bestuderen.

We kiezen voor het gemak $\vec{L}_1$ voor het eerste impulsmoment en $\vec{L}_2$ voor het tweede impulsmoment. Het doet er overigens helemaal niet toe of het hier gaat om een baanimpulsmoment of om een intrinsiek spinimpulsmoment, de formules zijn voor beide gevallen hetzelfde.

Impulsmomenten kan je gewoon vectorieel optellen zodat: $$ \hat{\vec{J}}=\hat{\vec{L}}_1+\hat{\vec{L}}_2 $$ Nu is het natuurlijk de vraag wat er gebeurt met de operatoren $\hat{J}^2$ en $\hat{J}_z$. Voor de operator van de $z$-richting is het logisch dat: $$ \hat{J}_z = \hat{L}_{1z} + \hat{L}_{2z}, $$ maar de relatie waaruit je $\hat{J}^2$ kan bepalen moet lastiger zijn. De lengte die volgt uit het kopstaart leggen van de twee vectoren hangt namelijk af van hun onderlinge oriëntatie.

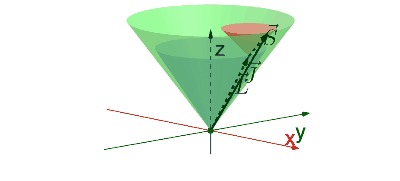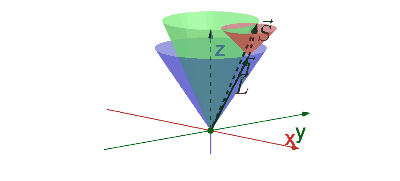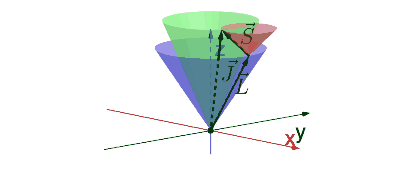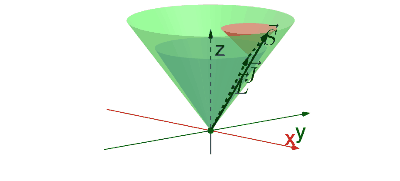
Bewijs

Werken we de term voor $\hat{J}^2$ uit, dan zien we:

$$ \begin{align} \hat{J}^2&=\hat{\vec{J}}\cdot\hat{\vec{J}}\\ &=(\hat{\vec{L}_1}+\hat{\vec{L}_2})\cdot(\hat{\vec{L}_1}+\hat{\vec{L}_2})\\ &=\hat{L}_1^2+\hat{L}_2^2+2\hat{\vec{L}_1}\cdot\hat{\vec{L}_2} \end{align} $$ Hier zien we dat de term $\hat{J}^2$ dus afhankelijk is van het inproduct van de twee vectoren. Dat inproduct is evenredig met de cosinus van de hoek.

Aan de ene kant kan je ervoor kiezen om de twee impulsmomenten apart te meten. In dat geval zijn de volledige set kwantumgetallen niets anders dan de dubbele set van een enkel impulsmoment: $$ \ket{l_1 l_2 m_1 m_2} $$ Hierbij staat $l_1$ voor het kwantumgetal voor het baanimpulsmoment van deeltje 1 en $m_1$ voor het magnetisch kwantumgetal in de $z$-richting van deeltje 1. In dit geval ben je echter de informatie over de hoeken tussen $\vec{L}_1$ en $\vec{L}_2$ kwijt. Deze informatie zit namelijk versleuteld in de $x$- en $y$-componenten van de vectoren, die niet commuteren met de $z$-component.

Aan de andere kant kan je ook kiezen om de twee impulsmomenten op te tellen tot een totaal impulsmoment. In dat geval is de volledige set kwantumgetallen gegeven door: $$ \ket{l_1 l_2 j m_j} $$ In dit geval is $j$ het kwantumgetal voor het baanimpulsmoment van de som van de twee deeltjes en $m_j$ het magnetisch kwantumgetal in de $z$-richting van dezelfde som. In dit geval weet je de lengte van de som van de impulsmomenten (gegeven door kwantumgetal $j$) en dus ook de hoek tussen de twee individuele impulsmomenten. Dan ben je echter de informatie over de $z$-component van de individuele impulsmomenten kwijt (gegeven door $m_1$ en $m_2$ in de andere basis).

Het is nu interessant om te zien hoe je tussen deze twee bases kan transformeren. Later zullen we dit zelfs regelmatig doen als we deze theorie gaan toepassen. In dat geval wil je de toestanden $\ket{l_1 l_2 j m_j}$ uitdrukken in $\ket{l_1 l_2 m_1 m_2}$ of andersom. Door de volledigheidsstelling toe te passen kunnen we eenvoudig inzien dat $$ \ket{l_1 l_2 j m_j} = \sum_{m_1,m_2} \ket{l_1 l_2 m_1 m_2} \braket{l_1 l_2 m_1 m_2|l_1 l_2 j m_j} $$ We zoeken dus naar de waarde van de termen $\braket{l_1 l_2 m_1 m_2|l_1 l_2 j m_j}$. Deze worden de Clebsch-Gordan coëfficiënten genoemd.

Deze coëfficiënten voldoen in ieder geval aan twee belangrijke regels:

$m_j=m_1+m_2$ en anders is de coëfficiënt nul.
$\lvert l_1-l_2 \rvert \le j \le l_1 + l_2$ en anders is de coëfficiënt nul.

Argumentatie

Het eerste punt is een natuurlijk gevolg van het feit dat $\vec{J}$ de som is van $\vec{L}_1$ en $\vec{L}_2$.

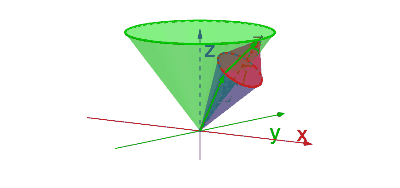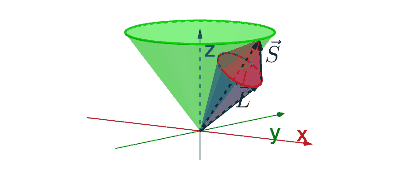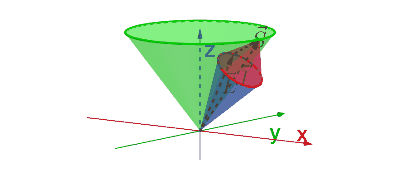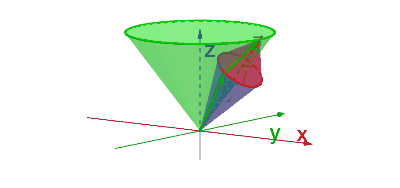
Voor het tweede punt moeten we iets beter kijken naar de toestanden waarover we het hebben. We hebben alle toestanden in de basis $\ket{l_1,l_2,m_1,m_2}$ hieronder op een systematisch manier geordend. Voor dit plaatje gaan we ervan uit dat $l_1=3$ en $l_2=1$, maar de redenering daaronder is voor het algemene geval uitgewerkt. We hebben daarin alleen aangenomen dat $l_1 \ge l_2$.

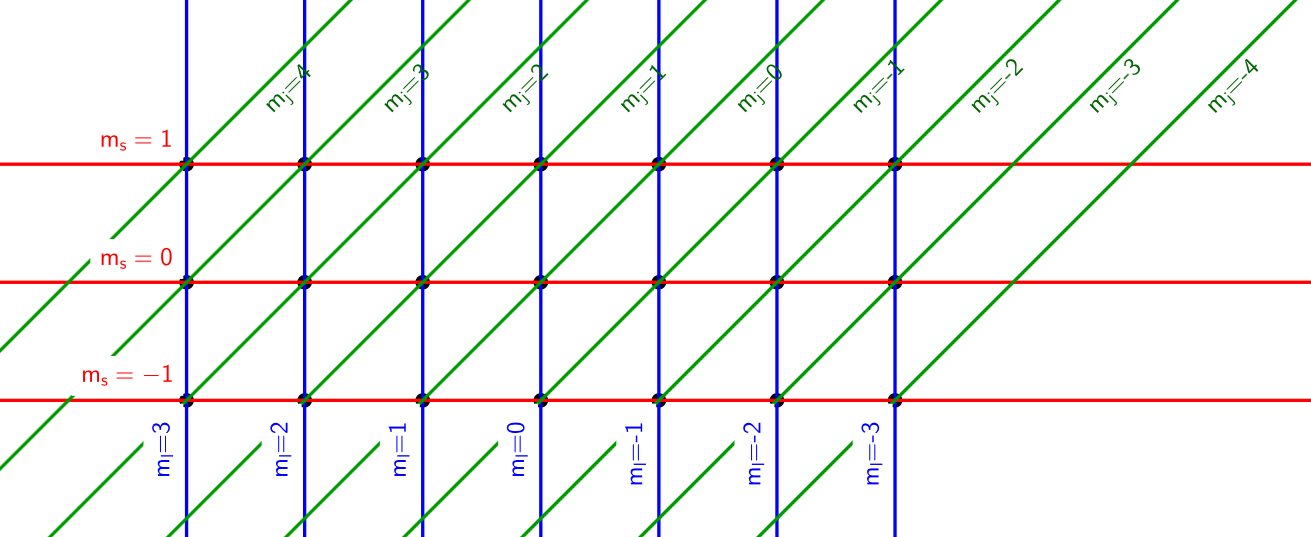
Begin bij de toestand $m_1=+l_1$ en $m_2=+l_2$. Voor die toestand moet gelden dat $m_j=+l_1+l_2$. Omdat je aan de andere kant weet dat $m_j \in \{ +j,\dots,-j \}$, moet er dus gelden $j=l_1+l_2$. De toestand $\ket{l_1,l_2,m_1,m_2}=\ket{l_1,l_2,+l_1,+l_2}$ komt dus overeen met de toestand $\ket{l_1,l_2,j,m_j}=\ket{l_1,l_2,l_1+l_2,+l_1+l_2}$. Om de notatie overzichtelijk te houden, laten we de termen $l_1$ en $l_2$ in de ket verder achterwege. Deze hebben toch telkens dezelfde waarde.

In de bovenstaande figuur kan je zien hoe we de rest van de redenering doorlopen. De deelruimte waarvoor geldt dat $m_j=l_1+l_2-1$ is een tweedimensionale deelruimte opgespannen door de vectoren bij de toestanden $\ket{m_1,m_2}=\ket{l_1-1,l_2}$ en $\ket{l_1,l_2-1}$. Als we deze deelruimte uitdrukken in een andere basis, moet deze deelruimte ook tweedimensionaal zijn. Er moeten dus twee waardes zijn voor $j$ waarbij $m_j=l_1+l_2-1$. Dat zijn natuurlijk de waardes $j=l_1+l_2$ en $j=l_1+l_2-1$.

Telkens als de waarde van $m_j$ met 1 verlagen, zie je in de figuur dat het aantal mogelijke combinaties van $m_1$ en $m_2$ met 1 toeneemt. Dat betekent dat er in de andere basis ook telkens een $j$-waarde bij moet komen om de dimensie van de deelruimte kloppend te krijgen.

Als $m_j$ de waarde $l_1-l_2$ heeft bereikt, dan komen alle mogelijke waarden voor $l_2$ in de combinaties voor de $\ket{m_1,m_2}$-basis voor. Er zijn dan $2 l_2 + 1$ combinaties. Dat betekent dat $2 l_2 + 1$ ook de maximale dimensie is voor de deelruimte behorend bij een waarde van $m_j$. Er zijn dus $2 l_2 + 1$ verschillende waarden voor $j$. Daaruit kan je inderdaad concluderen dat: $$ l_1-l_2 \le j \le l_1 + l_2. $$

Nu kan je ook verifiëren dat de totale dimensie van de toestandsruimte hetzelfde is voor de twee bases. De dimensionaliteit van $\ket{l_1,l_2}$-basis is aan de figuur gemakkelijk te herkennen als $(2l_1+1)(2l_2+1)$. De dimensionaliteit van de $\ket{j,m_j}$-basis is gegeven door: $$ \begin{align} \sum_{j=l_1-l_2}^{l_1+l_2} 2j+1 &= \sum_{j=1}^{l_1+l_2} 2j - \sum_{j=1}^{l_1-l_2-1} 2j + \sum_{j=l_1-l_2}^{l_1+l_2} 1\\ &=(l_1+l_2)(l_1+l_2+1)-(l_1-l_2-1)(l_1-l_2)+2l_2+1\\ &=4l_1l_2+2l_1+2l_2+1\\ &=(2l_1+1)(2l_2+1) \end{align} $$ De toestanden $l_1-l_2\le j \le l_1+l_2$ voldoen dus aan alle voorwaarden. De absoluutstrepen voor de algemene formule vangen ook de situatie af waarin $l_2 > l_1$.

Als je tussen deze twee bases wilt wisselen, wil je natuurlijk niet alleen weten welke coëfficiënten er ongelijk aan nul zijn, maar ook wat hun precieze waarde is. Dat is echter niet een berekening die je telkens opnieuw hoeft uit te voeren. Er zijn gewoon tabellenboeken waar je de juiste waarde kan aflezen.

De Clebsch-Gordan coëfficiënt bepaal je daaruit als volgt:

Vind de tabel die hoort bij de combinatie van impulsmomenten die je wilt weten.
Bepaal welke basis bij de rijen en welke bij de kolommen hoort.
Vind de juiste rij.
Vind je juiste kolom.
Neem het getal dat hier vermeld staat en neem de wortel hiervan.
Zet een minteken voor de wortel als dit vermeld staat.

Voorbeeld: Clebsch Gordan

In tabel 4.8 (blz. 226) van het boek van Griffith vind je een aantal van deze tabellen. We nemen er eentje over.

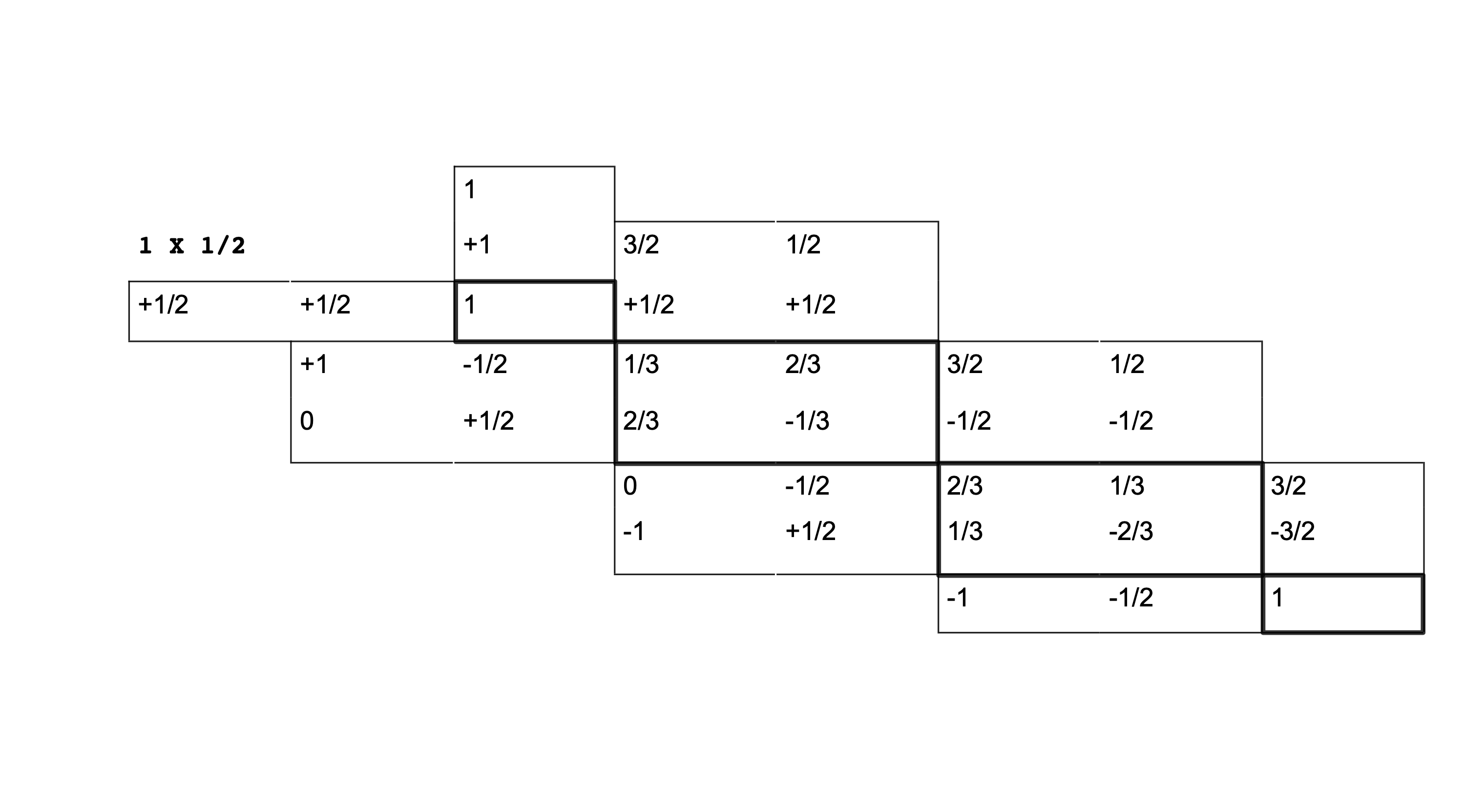
Dit is de tabel voor het geval waarin $l_1=1$ en $l_2=\frac{1}{2}$ (zoals linksboven vermeld staat). In eerste instantie is de tabel een beetje cryptisch, maar het zit heel logisch in elkaar. De blokken die dik omlijnd zijn, bevatten de gegevens voor de Clebsch-Gordan coëfficiënten. De blokken aan de linker- en bovenkant omschrijven de toestanden van de basis.

Ten eerste kan je inzien dat links de $\ket{m_1,m_2}$-toestanden staan vermeld, terwijl aan de bovenkant de $\ket{j,m_j}$-toestanden staan. Dat kan je zien doordat de waarde voor $j$ nooit negatief kan zijn (en verder alle rekenregels netjes gevolgd worden).

De coëfficiënt tussen de toestand $\ket{m_1,m_2}=\ket{0,+\frac{1}{2}}$ en $\ket{j,m_j}=\ket{\frac{1}{2},+\frac{1}{2}}$ is op deze manier $$ \Braket{m_1,m_2|j,m_j}=\Braket{0,+\frac{1}{2}|\frac{1}{2},+\frac{1}{2}}=-\frac{1}{3}\sqrt{3} $$

Op deze manier kan je de toestand $\ket{j,m_j}=\ket{\frac{1}{2},+\frac{1}{2}}$ uitdrukken in de $\ket{m_1,m_2}$-basis als: $$ \frac{1}{3}\sqrt{6}\;\Ket{+1,-\frac{1}{2}}-\frac{1}{3}\sqrt{3}\;\Ket{0,+\frac{1}{2}} $$